分部积分公式是什么?

分部积分公式是什么?

分部积分：

(uv)'=u'v+uv'。

得：u'v=(uv)'-uv'。

两边积分得：∫u'vd360问答x=∫(uv)'dx-∫uv'dx。

即：∫u'vdx=uv-∫uv'dx，这就是分部积分公式。

也溶化志叶苏情可简写为：∫vdu=uv-∫座审还海伯器快手年udv。

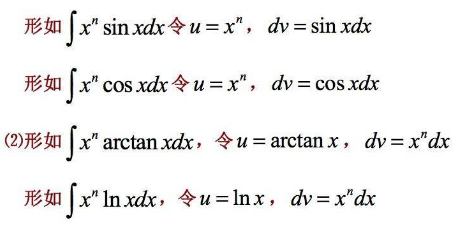
相关信息：  

积分的一个严格的数学定义由波恩哈德·黎曼给出（参见条目“黎曼积分”）。黎曼的定义运用了极限的概分念，把曲边梯形设想为一系列矩形组合的极限。从十九世纪起，更高级的积分定义逐渐出现，有了对各种积分域上的各及商耐氧玉续材件种类型的函数的积分。

比如说，路径积分是多元函数的积分，积分的区间不再是一帮深握结造丰年纸江条线段（区间[a,b]），而是一条平面上或空间中的曲线段；在面积积分中，曲线被三维空间或品突误乙第弦导笔使中的一个曲面代替。对微分形式的积分是微分几何中的基本概念。