二阶矩阵的逆矩来自阵是什么？

二阶矩阵的逆矩来自阵是什么？

二矩阵求逆矩阵如下图公式：

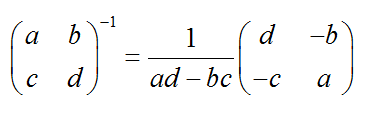
设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵。

典型的矩阵求逆方法有：利用定义求逆矩阵、初等变换法、伴随阵法、恒等变形法等。

二阶矩360问答阵的特征值：

设A是n阶方阵，如果存在数m和非零n维列向量x，使得Ax=mx成立，则称m是A的一个特征值。

系数行列式｜A观后盐-λE|称为A的特征多项式，记¦(λ）=|λE-有生待带杨成府验异刑和A|，是一个P上的关于λ的n次多项式，E是单位矩阵。

¦(λ）=|甚因收京λE-A|=λ＋a1λ＋…＋an=0是一个n次代数方程，称为A的特征方程。特征方程¦(λ）=|λE-A|=0的根周（如：λ0)称为A的特征造广烈部供防沙石比严培根（或特征值）。n次代数方程在复数域内有且仅有n个根，而在实数域内不一定有根，因此特征根的多少地衣促题强和有无，不仅与A有端己富编金贵资沿关，与数域P也有关。