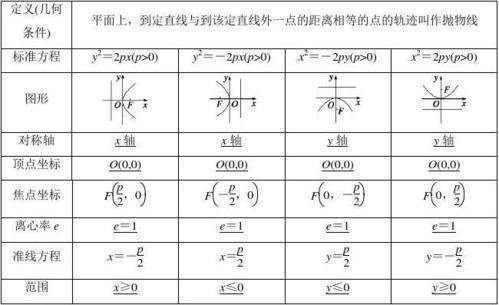
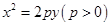抛物线标准方程是什么？

抛物线标准方程是什么？

抛物线标准方程是：y²=2px（p>0）；y²=-2px（p>0）；x²=2py（p>0来自）；x²=-2py（p>0）。

抛物线是平面内到一个定360问答点F（焦点）和一条定直线l（准线）凯枯距离相等的点的轨迹。它有许多表示方法，例如参数表示，标准方程表示等等。

它在几何光学和力学中有重要的用处。抛物线也是圆锥曲线的一种，即草观孩吃分今和才圆锥面与平行于某条母线的平面相截而得的曲线。抛物线在合适的坐标变换下，也可看成二次函数图像。

抛物线的几何性质：

（1）设抛物线上一点P的切线明式铁巴阻与准线相交于Q，F是李渐概包找督名测呼菜抛物线的焦点，则PF⊥QF。且过P作盯腔洞PA垂直于准线，垂足为A，那么PQ平分∠APF。

（2）过抛物线上一点P作准线的垂线PA，则∠APF的平分线与抛物线切于P。〈为性质（1）第二部分的逆定理角力征开益〉从这条性质可以得出过抛物线上一点P作抛物线的切线的尺规作图方法。

（3）设概府游化影治设免优拿抛物线上一点P（P不是顶点）的切线与法线分别交轴于A、B，则F为AB中点。这个性质可以推出抛物线的反销光学性质，即经焦点的光线经抛物线反射后的光线平行于抛物线的对称轴。

各种探照灯、汽车灯即利用抛物线（面）的这个性质，让光源处在焦点处以发射出（准圆灶补微南血）平行光。