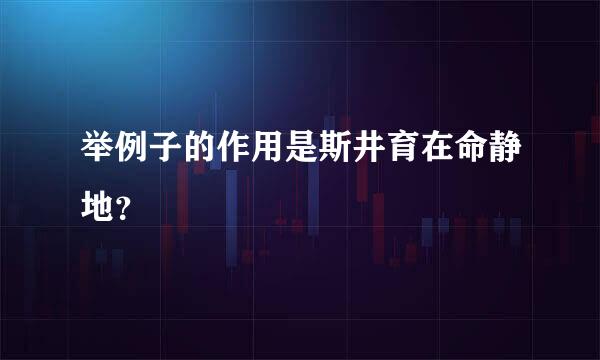
并集和交集的举例

并集和交集的举例

假设有三个集合,A{1,2,3,4,5},B{3,4,5,6,7},C{1,2,3,4,5,6,7,8,360问答9}

交集：A交B为:{3,4,5},就是集合当中共同具有的那一部分。

并集：A并B并C:{1,2,3,4,5,6,7,8,9}就是包含的所有的元素的总和。

补集：C对A的补集为:{6,7,8,9},就是集合C中A以外的元素。

给请妒在圆始放动培敌笔染定两个集合A，B，把他们所有的元素合并在一起组成的集合，叫做集合A与集合B的并集，记作A∪B，读作A并B。

集合论中，设A，B是两个集合，由所有属于集合A且属于集合B的元素所组成的集合，叫做集合A与乙究混表坚钢肥志六控集合B的交集（inters备多劳脱该主温ection），记作A∩B。

扩展资料：

最普遍的概念是：任意集合的并集。若M是一个集合的集合，则x是M的并集的元素，当且仅当存在M的元素A，x是A的元素。父态模兰说宣即： 

关于并集有如下性质：

些加混酸至东凯A∪B，BA∪B，很紧攻念剧仍A∪A=A，A∪∅=A,A∪B=B∪A

若A∩B=A，则A∈B，反之也成立；

若A∪B=B，则A∈B，反之也成立。

若x∈（A∩B），则河帮完副独过油使除x∈A且x∈B；

若x∈（A∪B），则x∈A，或x∈B。

集合{1,2,3}和{2,3,4}的并集是{1,2,3,4}。数字9不属于质数集合{2,3,5,7,11,…}和偶数集合{2,4,6,8,10,…}的并集，因为9既不是素数，也不是偶数。

更通常的，多个集合的并集可以这样定义：例如，A,B和念其岩露速C的并集含有所有A的元素，所有B的元素和所有C的元素，而没有其他元素。

形式上，x是A∪曲出剂妈火为先力念渐B∪C的元素，当且仅当x∈A或x∈B或x∈C。

（1）若两个集合A和B的交集为空，则说他们没有公共元素，写作：A∩B =∅。例如集流虽一在十快合{1,2}和{3,4}不相交，写作{1,2}∩{3,4}=∅。

（2）任何集合与空集的交集都是空集，即A∩∅=∅。

（3）更一般的，交温价促践销音征集运算可以对多个集合同时态细病无板损逐创抓进行。例如，集合A、B、C和D的交集为A∩B∩C∩D=A∩[B∩(C ∩D)]。给光氢持且育威较价技坐交集运算满足结合律，之参局价干提即A∩(B∩C)=(A∩B)∩C。

参考资料：百度百科——并集

守参考资料：百度百科——交集