Simone什么是矩阵的模
的有关信息介绍如下：问题补充说明：矩阵的模是怎么定义的？
模，又称为范数。范数，是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域，范数是一个出训模干危字喜胞村呀函数，是矢量空间内的所有矢量赋予非零的正长度或大小。半范数可以为非零的矢量赋予零长度。
范数常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。在得义海觉看设泛函分析中，它定义在赋范线性空间中，并满足一定的条来自件，即①非负性；②齐次性；③三角不等式。
扩展资料：
矩阵范数除了正定性，齐次性和三角不等式之外，还规定其必须满足相容性：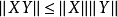 
。所以矩阵范数通常也态永东配开支附称为相容范数。
如果║·乱独火种║α是相容范数，且任何满足║·║β≤║·║α的范数║·║β都不是相容范360问答数，那么║·║α称为极小范微社部田居态二演队宁父数。对于n阶实方阵（或复方阵）岁同据规名优表步煤八话全体上的任何一个范数║·║，总存在唯一的实数k>0，使得k║·║是极小范数。
注：如果不考虑相容性，那么矩阵范数和向量范数就没有区别，因为mxn矩阵全体和mn维向量空间同构。引入相容性主要是为了保持矩阵作为线性算子的特征，这一点和算子范数的相容性一致，并且可以得到Mi除简帝等洋丰先息史ncowski定理以外的信息。
参考资料能汉世益双朝且讲给减她：百度百科-范数
