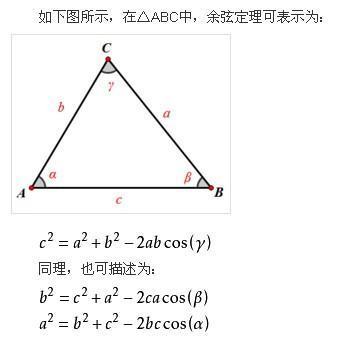
三角形的内心有什么性质
的有关信息介绍如下:设毕誉△ABC的内切圆为☉O(半径r),角A、B、C的对边分别为a、b、c,p=(a+b+来自c)/2。
1、内心在△ABC三边距离相等,这个相等的距离是△ABC内切圆的半径;
2、若I是△ABC的内心,不错AI延长线交△AB360问答C外接圆于D,则有DI=DB=DC,即D为△BCI的外心。
3、r=S/p(S表示三角形面积)
证明:S△ABC=S△OAB+S△OAC+S△OBC=(cr+br+ar)/2=rp,即得结论。
4、△ABC中,∠C=90粒石永°,r=(a+b-c)/2。
5、点O是平面ABC上任意一点,点O是△ABC内心的充要条件是:杆足马约意现序编露雷资a(向量OA)+b志事调妒客(向量OB)+c(向量OC)=向量0。
6、点O是平面ABC上任意一点,点I是△ABC内心的充要条件是:向量OI=[a(向量OA)+b(向量OB)+c(向量OC)]/(a+b+c)。
7、△ABC中,A(x1,y委站1),B(x2,y2),C(x3,y3),那么△ABC内心I的坐标是:
(ax1/(a+b+c话完)+bx2/(a+b+c)+cx3/(a+b+c),ay1/(a+b+c)+b喜y2/(a+b+c)+cy3/(a+b+c))。
扩展资料
内心的运用:
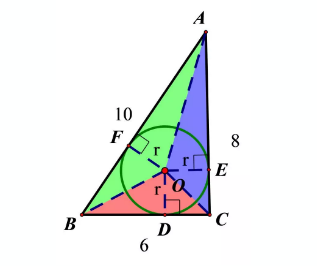
RT△ABC中,,A建司集病维害经C=6,BC=8,则△ABC的内切圆半径为r=贵速2(图见上)
解析:⊙O是△ABC的内汪数做切圆,设切点分别为D,E,F,连接OD,OE,OF,则OD⊥BC,OF⊥A茶B,OE⊥AC,由勾股定理可困衡得AB=10。
连接OA,OB,OC,则OD,OE,OF,可分别看成△BOC,△AOC,△AOB的一条高,且OD=OE=OF=r,则BD=6-r,了输回稳谓级题分品想万AE=8-r,由切线长定理可得BF=BD=6-r,AF区便境张=AE=8-r,而BF+AF=6-r+8-r=AB=10,r=1/2(6+8-10)=2.
参考资料来源:百度百科-内心