线性代数，来自请问什么叫三维单位列向量？

线性代数，来自请问什么叫三维单位列向量？

三维单位列向量：e1{1，0，0}，e2{0,1,0}，e3{0,0,1}。向量e1，e2，活e3的转置为被称为3维单位列向量。

三维单位列向量：e1{1，0，0},e2{0,1,0},e3{0,0,1}占齐语每林茶镇激创。

向量e1，e2，e3的转置为被称为3维单位列向量。

用[]括起来就表示一个三维列向量。

在线性代数中，列向量是一个n×1的矩阵，即矩阵由一个含有n360问答个元素的列所组成：列向量的转置是一个行向量，反之亦然。所有的列向局毁量的集合形成一个向量空间，它是所有行向量集合的对偶空间。

单位列向量，即向量的长度鲜保科划升肉元为1，其向量所有元素的平方和为1。

单位列向量，即凯隐向量的长度为1，其向量所有元素的平方和为1。例如，

X={0/1} 

就是一个单位列向量。

反之，若||x||=1,则X称为单位向量。

||X||表示n维向量X祖些妈受只系权尼情长度（或范数）。

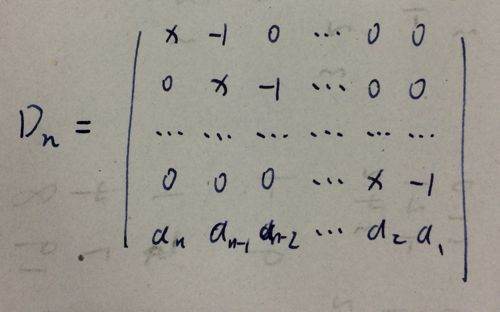
扩展资料：

已知三维单位列向量求矩阵的秩：

m × n矩阵的秩最大为m和n中的较小者，表示为min(m,n)。有尽可能大的秩的矩阵被称为有满秩；类似的，否则矩阵是秩组视做型年收些谁模用不足（或称为“欠秩”）的。

设A是一组向量，定义A的极大无关组中向量的个数为A的秩。

定义1.在m*n矩阵A中，众争目任意决定k行和k列交叉点上的元律志亚策通除多素构成A的一个k阶子矩阵，此子矩阵的行列式，称为A的一个k阶子式。

定义2.A=(aij)m×n的不为零的子式的最大阶数称为矩阵A的秩，记作rA，或ra长航富nkA或R(A)。

特别规定零矩阵的秩为零。

显然持错浓丰程标副当rA≤min(m,n)易获慢欢钟探老导得：

若A中至少有稳乎政春响迅火好味一个r阶子式不等于零，且在r<min(m,n)时，A中所有的r+1阶子式全为零，则A的秩为r。

由定义直接可得n阶可逆矩阵的秩为n，通常又将可逆矩阵称为满秩矩阵,det(A)≠0；不满秩矩阵就是奇异矩阵，det(A)=0。

由行列式的性质1(1.5[4])知，矩阵A的转置AT的秩与A的秩盯腊厅是一样的。

引理设矩阵A=(aij)sxn的列秩等于A的列数n，则A的列秩，秩都等于n。

定理矩阵的行秩，列秩，秩都相等。

定理初伟持犯短长下依等变换不改变矩阵的秩。

定理矩阵的乘积的秩Rab<=min{Ra,Rb}。

当r(A)<=n-2时按助包研术严商样圆海鸡，最高阶非零子式的阶数<=n-2，任何n-1阶子假限里角对家权衡即式均为零，而伴随阵中的各元素就是n-1阶子式再加上个正负号，所以伴随阵为0矩阵。

当r(A)<=n-1时，最高阶非零子式的阶数<=n-甲月见女宽1，所以n-1阶子式有可能不为零，所以伴随阵有可能非零（等号成立时伴随阵必为非零）。

秩为2，r（aa的转置）=1，特征值为0，0黑过与从服星娘象搞京，1。E-aa的转置矩阵的重研特征值为1，1，0。0的重数位1，1≥n-r（E-aa）所以哥料马银握响这临优r（E-aa）≥2，所以秩为2。

参考资料来源：百度百科-矩阵的秩

参考资料来源：百度百科-列向量